2016.08.02
楽しく遊べて、しかも使える道具を手に入れよう! -わくわくするベクトルの世界-
理数系科目に強い塾として知られるSEG。数学の専門塾としてスタートしただけに、数学の授業には独特の魅力があるという。聞けば、学校で教える範囲を超え、大学レベルにまで踏み込むこともあるとのこと。その魅力を実際に確かめてみた。
ちなみにレポーターは理系出身だが、卒業後は数学とはまったく縁のない世界にいるため、生活に必要な算数を除けば、高校までに蓄積した数学の知識はほとんど失われているといっていい。微分、積分、ベクトル、行列、三角関数、対数…どれも習った記憶はあるものの、それらがどんな概念で、どのように扱っていたのかについては、すっかり抜け落ちている。
高校1年生に戻って最初から学ぶつもりで、教室の末席についてみた。
授業の最後には、ベクトルは奥が深くて面白いと感じるはず

教室に入ると、すでに50人近い生徒のざわざわした熱気にあふれていた。高校1年生のクラスだというが、なぜかみな大人びて見える。担当の岡本先生が教室に入ってきても、そのざわざわ感は消えない。先生もその様子を気にかける様子もない。「気をつけ、礼」で始まる授業で学校生活を送ってきた身には、戸惑いが広がる。
「今日から平面ベクトルという新しい単元に入ります。前回は授業内で実力テストを実施しましたが、テストの結果は後ほど返します、お楽しみに。今日は復習テストはせず、いきなり授業に入っていきましょう。」 先生はこう言うと、黒板に何やら書き始めた。すると、教室内がスーッと静かになっていった。あえて今から授業の時間だと区切らなくても、SEGの生徒は必要なときには集中していくようだ。

「ベクトルという言葉は聞いたことがある人もいるかもしれません。一言でいえば、『矢印で表されるような量』全般を指す言葉で、たとえば、物理で学ぶ『力』や『速度』などといった量はベクトルです。数学で登場するベクトルとしては、『移動量』が挙げられます。高校の数学でベクトルと言ったら『移動量』のことを指すと思っておいて良いでしょう。」
そして、平面上の点A(1, 2)、点B(3,-5)を黒板に書いて、移動量についての概念をどんどん解説していく※(図A)。
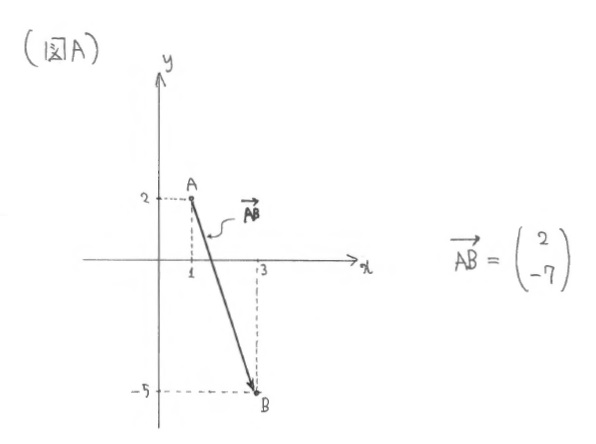
「この図でベクトル \(\overrightarrow{\rm AB}\) は、\(x\)方向に2、\(y\)方向に-7だけ進むような移動量であり、 \(\pmatrix{2\\-7}\) と書いたりします。」
「こんな移動量となんていうものに注目して何が面白いのかと思う人もいるかもしれません。確かに、最初の方はあまり面白くありません。しかし、今日の3時間目あたりにもなれば、移動量というものの見方はなかなか奥が深くて面白いなぁという気持ちになっていただけていることでしょう。では、ベクトルについて知っておくべき表記をいくつか紹介していきます。」
その後、ベクトルの足し算、ベクトルの実数倍について、平面座標に実例を示しながら、その概念を説明していく。
「たとえば、 \(\pmatrix{1\\2}+\pmatrix{-3\\4}\) と書いたら、「\(\pmatrix{1\\2}\) だけすすんだ後、さらに \(\pmatrix{-3\\4}\) だけすすむ」
という移動を表します。つまり、 \(\pmatrix{1+(-3)\\2+4}=\pmatrix{-2\\6}\) という移動を表します。

また、 \(3\pmatrix{1\\2}\) と書いたら「\(\pmatrix{1\\2}\) の3倍だけすすむ」という移動で、 \(-3\pmatrix{1\\2}\) と書いたら「\(\pmatrix{1\\2}\) と反対向きに3倍だけすすむ」という移動のことです。つまり \(3\pmatrix{1\\2}=\pmatrix{3\times 1\\3\times 2}=\pmatrix{3\\6}\)、 \(-3\pmatrix{1\\2}=\pmatrix{-3\times 1\\-3\times 2}=\pmatrix{-3\\-6}\) ということですね。
この様に、ベクトルという『移動量』の世界にも、ふつうの数の世界と同じように、『たし算』『なんとか倍』がありますし、『絶対値記号』もあります。たとえば、 \(\left|\pmatrix{3\\4}\right|\) と書いたらどんな意味になると思いますか?ふつうの数の世界と考え方は同じですよ。」
先生が初めて教室に質問を投げかける。すると生徒の1人が小声で「5」と答える。
「そうですね。値は5です。絶対値は、移動距離を意味しましたね。たとえば、 \(|-5|\) とは、数直線上で\(-5\) 進むという移動の移動距離のことで、\(|-5|=5\) でした。同じように \(\left|\pmatrix{3\\4}\right|\) とは \(\pmatrix{3\\4}\) という移動の移動距離のことなので、 \(\left|\pmatrix{3\\4}\right|=\sqrt{3^2+4^2}=5\) となります。」と先生が引き取り、黒板にこれまで解説したことをまとめていく※(図B)。

ここまでは、本当に流れるような授業だ。しかも、かなりペースが早く、距離の説明では、ピタゴラスの定理は全員が既知のこととして解説している。改めてこの授業のレベルの高さを実感した。
移動量という考え方に慣れよう
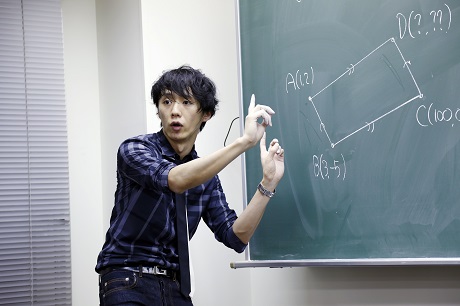
「では、移動量に注目することがどんな場面で便利か、例を見ていきましょう。」
応用例① A(1,2)、B(3,-5)、C(100,0)とする。四角形ABCDが平行四辺形になるようなDの座標は?
先生は、テキストの問題をやや変えてこんな問題を黒板に書く。早速ノート上で手を動かす生徒がいる。

「対角線の各々の中点が一致することからDの座標を求める、といったテクニカルな求め方もできますが、もっと素朴に解決できないかな?」 ある生徒が「BからAまでの移動と、CからDまでの移動が同じ!」と答えると、「そうです。BからAまでの移動量と同じ分だけCから移動すればよいだけですね。」 そう言うと、先生は、図を描きながら、
\(\overrightarrow{\rm CD}=\overrightarrow{\rm BA}=\pmatrix{1-3\\2-(-5)}=\pmatrix{-2\\7}\) であることを示した上で、C(100,0) から \(\pmatrix{-2\\7}\) だけ進んだ点 (98,7) がDであることを示していく。
「考え方に慣れるために、もう1つ例を一緒に見てみましょう。テキストの(105)の問題です。」
応用例② O(0,0)から、点A(12,9)を目指して距離10だけ進み、その後、点B(2,12)を目指して距離8だけ進んだ。辿り着いた点Pの座標は?
「ちょっと図を描きますね。OからAを目指して距離10だけ進んだ点をCとします。」※(図C)
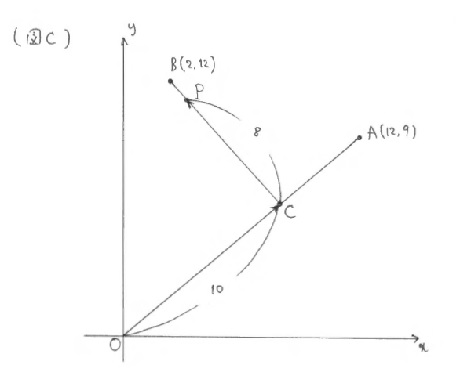
「Cの座標はすぐにわかりますね。OAの長さが15なので、OからAへの移動量の \(\dfrac{10}{15}\) 倍だけ、Oから移動すれば点Cにたどりつきます。つまり、※(図D)
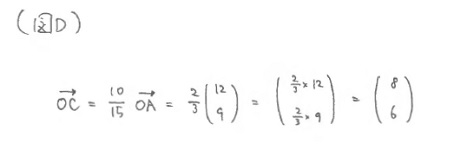
となって、Cの座標が (8,6) であることがすぐにわかります。そうなると、※(図E)

移動量について足し算などの表記を知っておくと、このように、答えを出すまでのプロセスを人に説明しやすくなりますね。」
授業開始から1時間以上が経過しただろうか。すると、先生は、先週のテストの答案を返却すると言う。微分総合演習という本格的なテストだったらしい。クラス内の空気がふっと緩み、当初の熱気が復活する。答案を返却されて「がんばります」という生徒や、「よっしゃ」という生徒など、喧騒が一気にヒートアップしていく。 「せっかくなので、平均点や最高点などの細かいデータ、1位の人の答案のコピーなども記念にさし上げます。良い刺激になってくれればうれしいです。僕自身SEGの生徒だったからわかりますが、SEGの良さは全力で数学を楽しんでいる仲間や大人に出会えることだと思います。周りの人からたくさん刺激を受けて、これからもますます数学に本気で打ち込んでくれたらうれしいですね。では10分間休憩です。」
移動量というものの見方を自分でもフル活用してみよう
休憩が終わって先生が入ってくると、今度は教室がスーッと静かになった。1時間あまりの授業で学ぶことに頭と体が慣れ、勉強する姿勢にすぐに切り替わった感じだ。 「1時間目は僕が1人でしゃべってしまったので、今度はみなさんにちょっと手と頭を使ってもらいましょう。」 そういうと、先生は黒板に問題を書き始めた。
Q1
A(2,3)、B(5,8)に対して
(あ) 線分ABを\(3:2\)に内分する点Pの座標は?
(い) 線分ABを\(3:2\)に外分する点Qの座標は?
Q2※(図F)
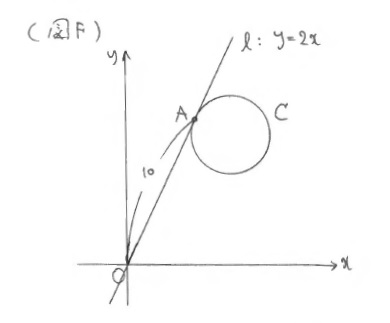
図のように、半径2の円 C が直線 \(l\) と点Aで接している。円の中心の座標は?
先生が書き終わらないうちに生徒たちは一斉に手を動かし始めた。これまで先生の解説を聞いていただけだったからか、自分で問題を解くことに喜びを感じているようにも見える。席の間をまわって生徒たちの手元を覗き込んでいた先生は、「早く終わってしまって余力がある人のために、もう1問」と言うと、次のように書き足した。
Q3 ※(図FFF)
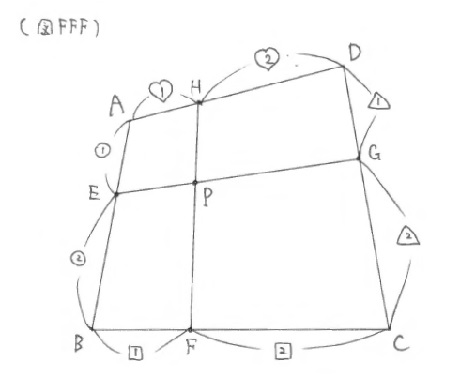
Pは、EG、HFを\(1:2\)に内分する点であることを示せ。

「他に方針は?」と聞かれ、楽しそうに手をあげる生徒。
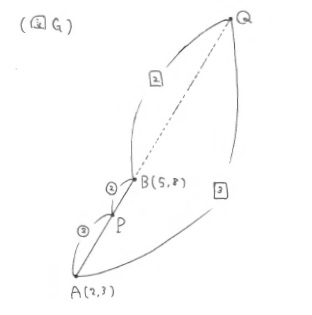
ときおり「ああ」とか、「そうか」という小声や、隣同士でぼそぼそと解き方を相談する声は聞こえるものの、教室内に落ち着いた、しかし凝縮した時間が流れていく。しばらく生徒の間をまわっていた先生は、「外分という言葉に、あまり馴染がない人もいるかもしれません。」というと、黒板に図を書き、「外分といったら線分の外にくるだけで考え方は同じです。PもQもAからの距離と、Bからの距離の比が\(3:2\)となる点です。」とヒントを出す。※(図G)

「Q3も座標を設定してみようかな」「あ、それは賢いね」など、互いに解き方を工夫する生徒たちの声が、あちこちから聞こえてくる。
「Q2は、座標の問題ですが、幾何的考察もおこたらずに。円と直線が接していたら、円の中心と接点を結んで \(90^{\circ}\) を意識することは基本中の基本ですね。」
しばらくすると、答え合わせが始まった。先生は、Q1に対して、ヒントで書いた図をもとに解説を始める。 「PもQも移動量を伸ばしたり、縮めたりする考え方でいけば、※(図H)

となります。 同様に、※(図I)
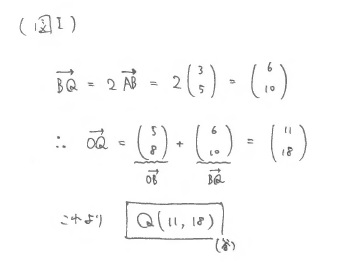
となりますね。」
「次にQ2ですが、円Cの中心をBとおいて、OからAに移動して、AからBに移動すると考えてみましょう。OからAに移動するには、\(l\)が伸びている方向、つまり、\(x\)方向に1進み、\(y\)方向に2進む移動と同じ向きに移動することになりますから \(\pmatrix{1\\2}\) の何倍かだけ移動することになります。何倍なのかも1時間目の要領ですでに分かりますね。」
先生はそう言いながら、解説を続ける。※(図J)
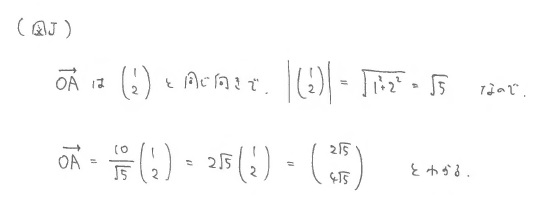
「次に、 \(\overrightarrow{\rm AB}\) という移動の向きは、 \(\pmatrix{1\\2}\) の向きを、時計回りに \(90^{\circ}\) 回した向きになりますから、円\(C\)の半径が2であることも加味すれば、無事解決しそうですね。※(図K)(図L)
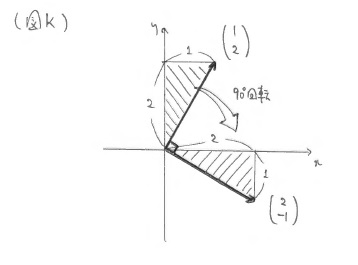

となります。この様に、『移動量に注目する』という考え方は素朴ではありますが、時として、強力な1つの手法となりうる、ということが分かりますね。」
公式は自分で作るもの
「Q1に補足しておきます。3時間目を楽しむための準備でもあります。」と言うと、先生は次のように板書した。※(図M)
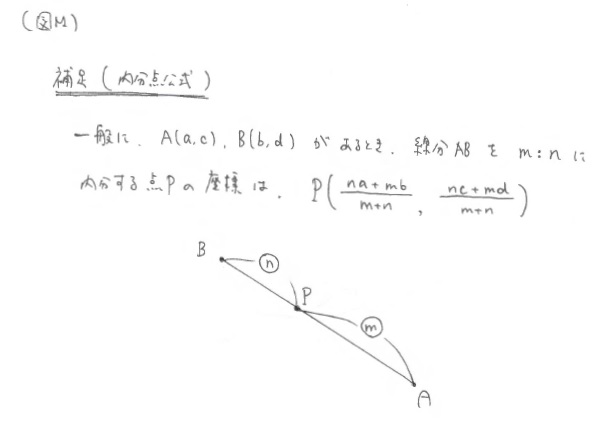
「この公式は覚えなくても、先ほどと同じ考え方で自分で作れます。※(図N)
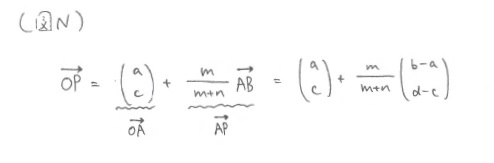
を計算して整理すれば、すぐに公式が得られますから覚える必要は特にありません。でも、覚えておくとちょっと面白い遊びができます。覚えるのであれば、この形よりも、次の形の方が覚えやすいです。」※(図O)
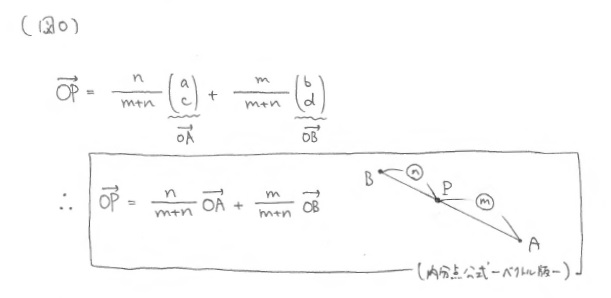
「ちなみにこれは、次の図を描いてしまうと当たり前ですね。」※(図P)
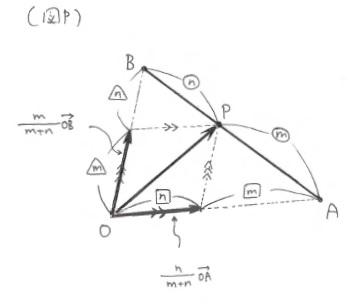
「3時間目が終わるころにはついつい覚えたくなっているかもしれません。内分点公式に限らず公式はその成り立ちを深く理解し、いつでも自ら作り出せるようにしておきましょう。そのうえで覚えるかその必要がないかは自分で判断しましょう。作れない公式を覚えて使うなんていうことは決してしないでくださいね。では、10分間休憩します。」
式の意味を考える
「次のような例をみると、内分点公式を知っててよかった、と感じるかもしれません。」
例 三角形ABCの3辺AB、BC、CAの中点L、M、Nとするとき、3直線CL、AM、BNが1点で交わることを示せ。
※(図Q)
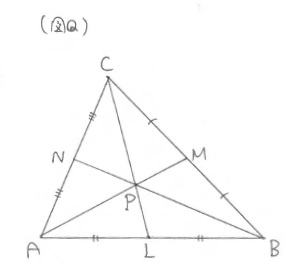
「3辺の中点を結ぶ中線が1点で交わり、その交点を『重心』と呼ぶのは、あまりにも有名な話ですが、そもそも、どんないびつな三角形でも、3本の中線が1点で交わることはどうやって証明するのでしょうか?という問題ですね。初等幾何で本来証明すべきことなのかもしれませんが、ここでは内分点公式とベクトルの考え方を使って証明したいと思います。中点は辺を1対1に内分する点だと考えて内分点公式を使っていきます。」※(図R)

「この証明の要点をまとめると次のたった4行の式変形に集約されます。」※(図S)
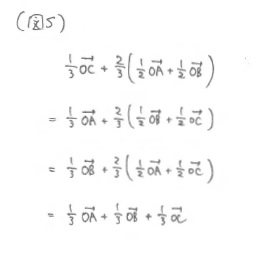
「式だけでみると、 \(\dfrac13\overrightarrow{\rm OA}+\dfrac13\overrightarrow{\rm OB}+\dfrac13\overrightarrow{\rm OC}\) という式が3通りに書けるというだけの話なのですが内分点公式をからませてこの式の幾何的意味を考えてみると、これがそのまま3中線が1点で交わることの証明になってしまう、というのが何とも面白いですね。
こんな話を聞いてしまうと、いろいろと遊んでみたくなりませんか?最後はちょっとテキストから脱線しちゃいましょう。
たとえば、 \(\dfrac14\overrightarrow{\rm OA}+\dfrac14\overrightarrow{\rm OB}+\dfrac14\overrightarrow{\rm OC}+\dfrac14\overrightarrow{\rm OD}\) なんていう式からスタートしてテキトーに式変形をしてみると何が起こるのでしょう。」※(図T)

「これが何か面白いことを意味していたりはしないかな?式の意味を考えてみよう。」 すると、ある生徒が「あ!2時間目のQ3とちょっと似た定理になってる!」 と素早い反応を返す。
「そうですね。四角形ABCDがあったとき2行目の式は、原点Oから、ABの中点KとCDの中点Mの中点への移動量で、3行目の式は原点Oから、BCの中点LとADの中点Nの中点への移動量です。これらが一致するということは、KMの中点とLNの中点は一致することがわかります。」※(図TT)
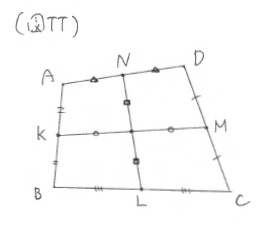
「たった3行の式変形から『どんな四角形でも向き合う辺の中点を結ぶと各々の中点で交わる』というちょっとした定理が作れてしまいました。」
「おお!」と生徒から歓声が上がる。「これを真似していろいろ試してみると面白そうですね。みなさんなら、他にどんな式を試してみたいですか?」
すると生徒は「テキトーに \(\dfrac1{10}\overrightarrow{\rm OA}+\dfrac2{10}\overrightarrow{\rm OB}+\dfrac3{10}\overrightarrow{\rm OC}+\dfrac4{10}\overrightarrow{\rm OD}\) !」
「じゃあ、 \(\dfrac15\overrightarrow{\rm OA}+\dfrac15\overrightarrow{\rm OB}+\dfrac15\overrightarrow{\rm OC}+\dfrac15\overrightarrow{\rm OD}+\dfrac15\overrightarrow{\rm OE}\) !」と好奇心旺盛だ。
すると、黙々とノートに計算をしていた生徒が急に顔をあげて、
「先生、 \(\dfrac19\overrightarrow{\rm OA}+\dfrac29\overrightarrow{\rm OB}+\dfrac49\overrightarrow{\rm OC}+\dfrac29\overrightarrow{\rm OD}\) がとても面白いことになります!」
とやや興奮気味。
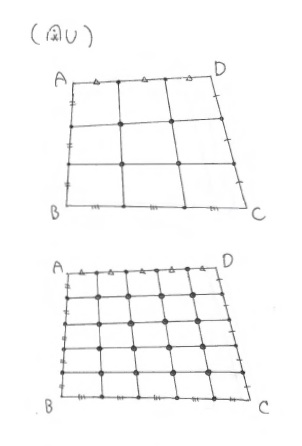
お、気づきましたか。そうです、その式からは、なんと『どんな四角形でも、向かい合う辺の3等分点を結ぶと各々の3等分点で交わる』という定理、つまり、2時間目のQ3にたどりつきますね。一般に\(n\)等分点に拡張することもできてしまいます。これはみなさんへのおみやげとしましょう。※(図U)」
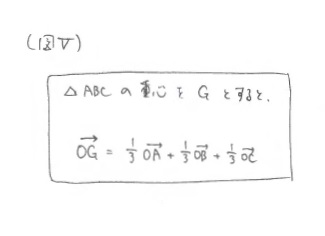
「内分点公式もこんな風に使うとなかなか面白い遊び道具です。さっきみなさんが言ってくれた式からも素敵な定理が作れそうですね。力作ができたら僕や友達にどんどん自慢してください。あっ、つい脱線してしまい忘れていましたが最初の重心の話の過程から得られる次の事実も、公式としておきます。これは一度見たら忘れませんね。」※(図V)
遊び心をもって数学を楽しもう
ここで終わりかと思ったら、先生は「あっ!ちょっといいこと思いついた。」
といいながら、 \(\dfrac16\overrightarrow{\rm OA}+\dfrac16\overrightarrow{\rm OB}+\dfrac16\overrightarrow{\rm OC}+\dfrac16\overrightarrow{\rm OD}+\dfrac16\overrightarrow{\rm OE}+\dfrac16\overrightarrow{\rm OF}\) という式を提示した。
黙々と式を変形させていく。「これはすごい!」と生徒たちがざわつく。そして、『平面上に6つの点があるとき、6点から3点を選んで作った三角形の重心と、残りの3点で作った三角形の重心を結ぶ線分は、最初の3点の選び方によらず、必ず定点を通る』という定理が得られることを生徒が指摘した。遊び感覚で楽しみながらも、生徒たちには自然と「式の意味を考える」姿勢が身についたようだ。
「定理や公式は人から教えられてそれを意味も分からず覚えて機械的に使うものではありません。『自ら発見し作るもの』なのだということがよく分かりましたね。それに必要なのはほんの少しのひらめきと『遊び心』です。何か新しい道具を手に入れたら『これは何に使えるかな、いろいろ試してみよう』という感じで、いろいろと遊んでみてほしいですね。そして、問題を作って友達や先生に出題してみるとか、そんな風にしてこれからもますます数学を楽しんでいってくれたらうれしいです。では今日はこれで終わります。」 先生はこう言って、何枚かプリントを配った。準備ができた生徒から一人ひとりと帰り始める。しかし、何人かは先生を囲んで議論を続けていた。
3時間を超す授業、しかも内容豊富な濃密な時間に、レポーターの頭はクラクラしかけている。だが、不思議なことに、ベクトルの概念と使い勝手の良さは、十分に理解できている。 それにしても、これまでに一度も、数学で“遊ぶ”という捉え方をしたことがなかったことに気がついた。高校時代にこんな授業を受けてみたかった…というのが正直な感想だ。残り5回の授業を受講し続ければ、きっとベクトルの魅力、いや数学の魅力にもっとはまっていくだろうとも感じた。もちろん、生徒たちは……いわずもがなだろう。