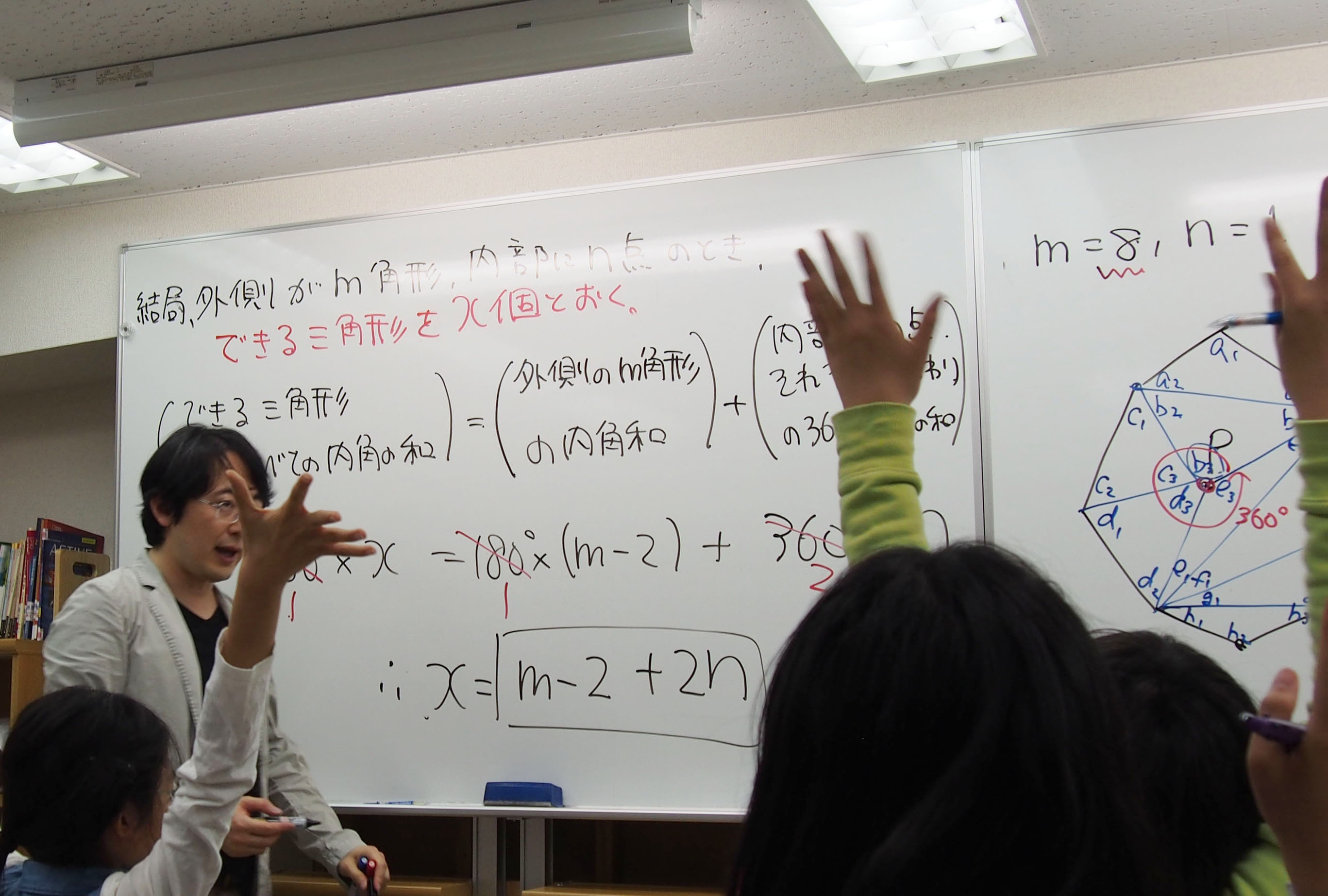2015.01.23
教えたいのは式変形じゃない。数学の「かっこよさ」だ。
数学専門塾としてスタートしたSEG。数学の授業のレベルの高さは全国トップクラスだ。授業の合間に、中学2年生がピタゴラスの定理を使った証明を「遊び」でやっている姿を見かけたときは、自分との差に感嘆したのだった。
私(矢部)は、Websiteの運営会社を経営している。ふとした縁でSEGの古川代表と知り合い、今回、SEGの授業の取材と執筆を依頼された。しかし、私事で申し訳ないが、私は算数がきらいだった。小学3年生の時、いつも宿題をやらずに授業が始まり、答え合わせの間、机の上に正座させられていた。保護者会でその事実を知った父は、恥ずかしくて顔を上げることができなかったそうだ。本当に申し訳ない。数学の世界が少しも分からないまま高校生になり、2次関数のテストで5点をとった時、母が真っ青になって家庭教師を探してきたことを覚えている。そんな私に、「数学が嫌いだった人の視点で正直な感想を書いてくれ」との依頼であった。
引き受けたものの、数学オンチの私は、中学1年生のクラスとはいえ、理解する自信がなかった。
間違いを消して、なかったことにしたら、また同じことを繰り返すぞ
復習テストでみんなが間違えやすかったところを確認。
何度も確認をすることで深い理解を促す。
緊張した面持ちで教室に入ると、数学の授業前とは思えないくらいの、明るい声が飛び交っている。男子生徒7名、女子生徒5名のこじんまりとしたクラスだ。
担当の佐藤太郎先生は、出席をとり終わったら宿題を回収し、復習テストを始めた。1次方程式、連立方程式の問題が並ぶ。先生が生徒の机を回り、正解には◯を、不正解にはどこが間違っているかをチェック。間違いに気づいてあわてて消しゴムを使う生徒に対して、
「間違ったところを消しゴムで消さない。どこを間違ったのかが分かるように」と指導。
「間違いを消して、なかったことにしたら、また同じことを繰り返すぞ」
こうやって数学の学習方法を一つひとつ身につけていくのだろう。
テストの解答を見ながら、みんなが間違っているポイントを整理。先週の授業のポイントを確認する。
「思い出した!」とぱっと明るい顔で喜ぶ生徒たち。
このクラスの生徒たちは、とにかく元気が良い。授業中でも分からないことは「分かんない!」と叫んだり、「先生、字がきたないよ」とツッコミをいれることもしばしば。
時には集中力を欠いて叱られたり、ふざけすぎてなだめられることもあるが、基本的には真摯に授業に取り組んでいる。数学の授業というと、黙々とペンを走らせるイメージがあったが、このSEGのクラスは一味違うようだ。
答にたどりつく方法は何通りもある

復習を終え、ここからが本題。今日のテーマは「不変量」。
先生がみんなに問題を出す。ホワイトボードに目を向けて集中する生徒たち。
\(m\)角形の内角の和は\(180° × (m − 2)\) で求められる。
どう証明しますか?
瞬時に一人の生徒が、「三角形に分けて内角の和を足す!」と解答。あっさり証明できた……!
[方針1]
\(m\)角形を\((m − 2)\)個の三角形に分けて、一つひとつの三角形の内角の和\(180°\)を\((m − 2)\)個分足す。
「他に方針は?」と聞かれ、楽しそうに手をあげる生徒。
「他には?」と、さらに答えを促す先生。
生徒の手が挙がり、これもあっさり「方針2」が決まる。
[方針2]
各頂点ごとに、内角と外角の和が\(180°\)。すべての頂点で足すと\(180° × m\)。ここで、
外角の和が\(360° = 180° × 2\)なので、これを引いて内角の和は\(180° × m − 180° × 2\)。
つまり、\(180° × (m − 2)\) になる。
「他には~?」と楽しそうに笑う先生。考えこむ生徒たち。
「こうしたらどうかな?」
「それだとダメだよ」
と生徒同士で、意見を言いながら方針を探していく。
先生がヒントを出す。
「真ん中に点をいれて……」とアイデアを話す生徒。
にわかに盛り上がる教室。
「外角を使わずに、方針2の
\(180° × m − 360°\)
と同じ式って説明できない?」
一人の生徒が「あっ」と小さくつぶやき、「真ん中に点をとったら……」とアイデアを出す。他の生徒も気がついたようで、
「そういうことか!」
「すごい、いい発想!」
「天才!」
と声があがる。
[方針3]
内部に点\({\rm P}\)をとり、△\({\rm P}{\rm A}_n{\rm A}_{n + 1}\)と\(m\)個の三角形に分け、\({\rm P}\)のまわりの360°を引く。(\({\rm A}_1,{\rm A}_2,……\)は\(m\)角形の頂点)
「この3つの考え方、どれも大事な考え方で、このあとの授業で役に立ちますからね」
と先生が念を押す。
突然ゲームが始まった。なんだか楽しそう
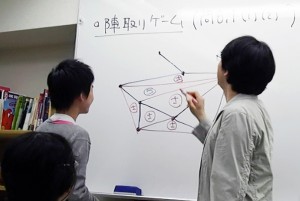
ルールを説明しながら、まずはデモンストレーション。
ここで「陣取りゲームをやってみましょう」と先生が言って、がらりと雰囲気が変わる。数学の授業で、ゲーム??
ルールは以下のとおり。
【陣取りゲームのルール】
(1)図のように平面上に8つの点がある。
(2)2人で交互に、1本ずつ点と点を線分で結んでいく。ただし、すでに引いた線分と交差してはいけない。
(3)内部に(頂点以外の)点を含まない三角形ができあがったら、自分の陣地として確保できる。
(4)線分がもう引けなくなったら、ゲームは終了。
(5)終了時に、とった三角形の多い人が勝ち。

テキストには点の配置の違うゲームが(1)~(5)まで
用意されている。
ルールが理解できたら、ペアになってテキストにある図を使って陣取りゲームのスタート。
「うーん、どこに引こう……」
「勝った!」
「負けた~!」
「後攻が有利じゃない?」
と、楽しそうな声が教室中に響きわたる。
みんな真剣に考え、ゲームに熱中している。
テキストには、点の配置が違う5つのゲームが載っている。点はどれも8つだ。
5つすべて終わったら、先攻後攻を入れ替えてもう1回戦。
みんなの勝負が決まったところで、先生がどちらが何個の陣地をとったかの勝敗を書き出した。
「勝ったり負けたりはいろいろだし、どんな三角形ができたかもいろいろだけど、この勝敗表には、なにか『不変量』がないかな?」

先生が問うと、生徒たちが
「全部で9個になる!」
と答える。
たしかに、三角形の描き方はそれぞれなのに、ゲーム(1)と(2)の8つの点では、陣地となる三角形の合計が9個になる。
なぜだろう?
他の配置の(3)~(5)の三角形ではどうだろうか?
みんなのゲームの結果を確認すると、(3)のゲームでは三角形は8個、(4)は10個、(5)では11個となることが分かった。
配置が変わると三角形の総数は変わるけれど、配置が同じなら三角形の総数は一定だ。
そこで新たな疑問が発生してくる。
これらの8つの点の配置のうち、何が三角形の総数を決めているんだろう?
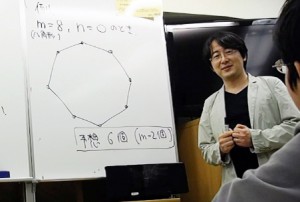
「さあどうする?」と疑問を投げかける先生。
考えこむ生徒を見て、ちょっと嬉しそう。
全員で、もう一度テキストをながめる。
「あ、これ、多角形だ!」
一人の生徒が思いつく。
(1)(2)は、五角形の頂点と内部の点が3点
(3)は六角形の頂点と内部の点が2点
(4)は四角形の頂点と内部の点が4点
(5)は三角形の頂点と内部の点が5点
ここまで分かったことをまとめると、
「できる三角形の総数は、外側が何角形か、内部の点がいくつあるかで決まる」
ということ。
法則があることは分かった。どうしてそうなるかの証明は?
さて、これが最後の問題。
外側が\(m\)角形で、内部にある点が\(n\)点のとき、できる三角形の総数を\(m\)と\(n\)の式で表し、どうしてそうなるかを証明せよ。
首をかしげる生徒たち。
先生が助け舟をだす。
「まずは仮説を立ててみよう。仮に、\(m = 8\), \(n = 0\)だったらどうだろう? やってみると、6個の三角形ができる。\(6\)個。つまり、\(m − 2\)だよね」
「八角形で、内部の点が0だったら、おそらく答は6個。この6個が変わらない量、つまり『不変量』であることを証明したい。さあどうする?」
再び静まり返る教室。さすがの生徒たちも眉をしかめている。ため息とともに「分かんない……」の声。
悩んでいる生徒を見てニコニコしながら、先生がヒントを出す。
「答とは別の、すでに知られている不変量を使うと、うまく説明できるよ」
懸命に考える生徒たち。私も一緒になって考える。答はもちろん出てこない。
「どんな風に分けようが、変わらない何かがあるんだよ。多角形で形によらない不変量って何があった?」
生徒たちが思い思いに答える。
「辺の数」「頂点の数」「対角線の数」「内角の和……」 「あ、内角の和!?」
先生がさらに進める。
「どんな風に頂点を結んでも、そこでできるそれぞれの三角形の内角は、ぜんぶ八角形の内角に集まってるよね。ということは、できた三角形が何個でも、そのすべての内角の和は、八角形の内角の和と一致するはずですね」
「あーーー!」
「分かったー!」
一斉に教室が歓喜に湧く。
先生は得意げに「ちょっと数学っぽくてかっこいい証明だと思いませんか?」と笑う。
たしかに、なんだかかっこいい……!
できる三角形を\(x\)個とおく
できた三角形の内角は、外側の八角形の内角を分けたものなので……
できた三角形\(x\)個すべての内角の和 = 外側の八角形の内角の和
\(180° × x = 180° × (8 − 2)
x = 6\)
さらに、証明は続く。
「これをふまえて、内部の点が増えたときのことを考えてみよう。
たとえば、\(m = 8, n = 1\)の場合はどうだろうか?
先ほど、八角形の中にできる三角形の内角は、八角形の内角に集まることが証明できた。内部に1点が加わると、すべての三角形の内角の和はどうなるだろう?」
生徒が答える。「\(360°\)増える!」
「そう、八角形の内角の和と点のまわりの\(360°\)ですね」
(できた三角形\(x\)個すべての内角の和)=(外側の八角形の内角の和)+(内部の点Pのまわりの360°)×(内部の点の数)
式で表すと、
\(180° × x = 180° × (8 − 2) + 360° × 1 \)
\(∴x = (8 − 2) + 2 = 8 \)
まとめると……
外側が\(m\)角形、内部にある点が\(n\)点のとき、できる三角形を\(x\)個とおく。
(できる三角形のすべての内角の和)=(外側の\(m\)角形の内角の和)+(内部の点 それぞれのまわりの360°) × (内部の点の数\(n\))
より、
\(180° × x = 180° × (m − 2) + 360° × n \)
\(∴ x = m − 2 + 2n個 \)
「多角形の中の陣取りゲームでできる三角形の個数には、こんな数学が隠れているんだよ」という先生の言葉に、教室中から歓声があがった。
答が理解できた生徒たちは、実に楽しげだ。見学者である私も充分に楽しかった。
「数学のかっこよさ」をみつけるためのストーリー
夢中になってゲームをすること、その中から疑問を見つけること、その疑問を解こうと懸命に考えること、そして答が分かったときの達成感。このストーリーには、勉強という枠を超え、人を成長させるあらゆる要素が含まれている……と考えるのは大げさだろうか。
私たちを行動させる動機は、とても単純だ。おもしろいか、おもしろくないか。かっこいいか、かっこよくないか。そういった感情の差異が、すぐさま行動にはねかえる。
自らやるか、命令されてやるか。あるいは、やらないか(かつての私のように……)。
その結果は明白だ。
この授業で見つけた「数学のかっこよさ」という切れ端は、彼らの中で、もっともっと大きく広がっていくだろう。